수식이 깨질 경우 새로고침을 눌러주세요.¶
Probability for Data-Science ⑥¶
Fat tail¶
데이터 분석 실무에서는 자연에서 발생하는 현상 중 많은 것들을 정규 분포를 따르는 확률 변수로 모형화하여 사용하고 있다.
그러나 이러한 데이터들을 자세히 살펴보면 실제로는 정규분포보다 양 끝단의 비중이 더 큰 것을 알 수 있다. 이를 fat tail 이라고 한다.
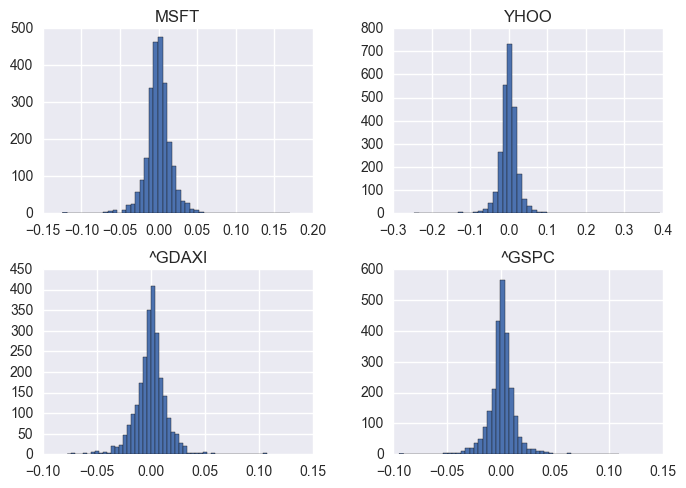
ex) 주식 데이터의 예
- 히스토그램을 그려서 자료 분포를 본다.
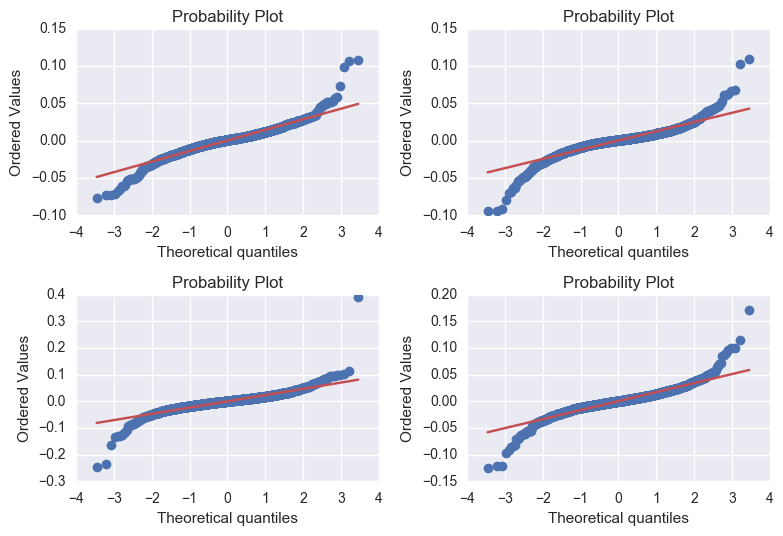
- Q-Q 플랏을 그려보고, 정규 분포와 비교해본다.
student-t distribution 분포¶
$$ x \sim f(x) \propto \left(1+\frac{(x-\mu)^2}{n\sigma^2} \right)^{\!-\frac{n+1}{2}} $$Parameter
- 표본의 평균, 표본의 분산, 자유도(degree of freedom, n)
- 표본에서 평균, 분산을 추정하는 분포이므로 자유도라는 모수를 추가적으로 갖는다.
$$ \bbox[15px, border:2px solid blue]{f(x) = \frac{\Gamma(\frac{\nu+1}{2})} {\sqrt{\nu\pi}\,\Gamma(\frac{\nu}{2})} \left(1+\frac{(x-\mu)^2}{\nu\sigma^2} \right)^{\!-\frac{\nu+1}{2}}} $$$$ \nu \text{는 nu라고 읽으며 자유도를 나타낸다.} $$∴ 스튜던트 t 분포의 확률 밀도 함수는 다음 수식에 의해 정의된다.
Mean
- 평균은 정규분포와 동일하게 mu $$\mu$$
Variance: $$\text{Var}[x] = \dfrac{n\sigma^2}{n-2}$$
t 분포의 특징
- 자유도가 증가할수록 가우시안 정규 분포로 수렴
- 자유도가 클수록 Sample 수가 많음으로, C.L.T에 따라 수렴
- 자유도가 낮으면 가우시안 정규 분포보다 분산이 크다. (fat fail)
- 정규 분포의 sample(표본)의 합이다.
scipy를 활용하여 스튜던트 t 분포의 확률 밀도 함수를 그려보자.¶
# -*- coding: utf-8 -*-
import seaborn as sns
import pandas as pd
import scipy as sp
import matplotlib as mpl
import matplotlib.pylab as plt
import numpy as np
%matplotlib inline
# n = 자유도, mean = 평균, scale = 표준 편차
sp.stats.t(df=n, loc=mean, scale=std)
plt.figure(figsize=(12,8))
# (-4, 4)에서 100개 점을 찍고 plot에 넣으면 이 점을 연결한다.
x = np.linspace(-4, 4, 100)
# 여기서는 df = 자유도
for df in [1, 2, 5, 10, 20]:
f = sp.stats.t(df=df)
plt.plot(x, f.pdf(x), label=("studen-t (df = {})".format(df)))
plt.plot(x, sp.stats.norm().pdf(x), label="Normal", lw=5, alpha=0.5)
plt.legend()
plt.show()
자유도가 높을 수록 정규분포와 가까워짐을 확인할 수 있다.¶
$$ t = \frac{\bar{x} - \mu}{s\;/\sqrt{n}} \sim t(n - 1) $$$$ \bar{x} = \frac{x_1+\cdots+x_n}{n} $$$$ s^2 = \frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})^2 $$가우시안 정규 분포로부터 얻은 n개의 sample이 있다. $$ x_1, \cdots, x_n$$
sample 평균을 sample의 표준편차로 정규화한 값은 df = n-1인 스튜던트 t 분포를 따른다.
여기에서 중요한 점은 표본의 표준편차로 나누었다는 것이다.
정규 분포로부터 얻은 sample의 평균은 그 자체로는 항상 정규 분포를 따른다.
sample의 표준편차라고 하는 다른 확률 변수로 나누는 과정에서 정규 분포가 아닌 스튜던트 t분포를 따르게 된다.
cf
(이론적 표준 편차라는 상수로 나눈) sample 평균은 원래대로 정규 분포를 따른다. $$ \frac{\bar{x} - \mu}{\sigma\;/\sqrt{n}} \sim N(0,1) $$
이 정리는 정규 분포의 기댓값에 관한 각종 검정(testing)에서 사용된다.¶
t분포 시뮬레이션¶
Ex)
가우시안 정규분포 N(1, 4) 에서 100개를 sampling 하자.
이것을 2,000번 반복하자.
그러면, 표본 평균은 2000개가 나올 것이고, 이로 인해 2,000개의 t값을 계산할 수 있다.
여기서 자유도는 2,000인가? 100인가?
100 !!
∵ 자유도는 하나의 t값을 구할 때 필요한 값이다.
t(100-1)의 분포 vs 2,000개의 t값으로 그린 히스토그램과 그 히스토그램에 fit된 그래프를 비교해보고, t값이 t분포를 따르는지 확인해보자.
아래 코드는 매트릭스를 활용하여 계산할 것이며, 한번에 2,000개의 t값을 구할 것이다.¶
참고. 매트릭스로 여러값을 한번에 구할 때는 매트릭스를 직접 그려보면서 코드를 같이 짜면 실수를 하지 않는다.
# N(1, 4)에서 100개 샘플링을 2,000번 반복
mu = 1
sigma = 2
f_normal = sp.stats.norm(mu, sigma)
# N(1, 4)에서 생성된 난수 매트릭스 (100, 2000)
N1 = 100
N2 = 2000
X = f_normal.rvs(size=(N1, N2))
# 행렬의 열을 다 더한 후,
x_bar = X.sum(axis=0) / N1
s = np.sqrt(((X - x_bar) ** 2).sum(axis=0) / (N1 - 1))
t = (x_bar - mu) / (s / np.sqrt(N1))
print(t, len(t))
위처럼 2000개의 t값을 구할 수 있다.¶
- 이제 t분포와 t값 2000개로 그린 선을 비교해보자.
f_t = sp.stats.t(N1 - 1)
xx = np.linspace(-6, 6, 100)
plt.figure(figsize=(12,6))
plt.plot(xx, f_t.pdf(xx))
sns.distplot(t, kde=False, fit=sp.stats.t)
plt.legend(["Student-t(N-1)", "Histogram"])
plt.show()