분포의 대표값에 대해 알아보자.¶
Sample 평균¶
$$ m = \bar{X} = \dfrac{1}{N}\sum_{i=1}^{N} x_i $$$$\bar{X}$$표본 평균이라고도 함
sample
- 정확히는 이미 가지고 있는 자료 값의 집합이 어떤 확률 모형 또는 모집합으로 부터 생성된 것이라는 가정하에 부르는 용어
- 데이터 분석에서는 유한한 개수의 데이터 집합으로 통용된다.
모집단에서 sampling을 할 때마다, sample mean의 값은 달라진다.
샘플링 할 때마다 샘플 평균이 예측할 수 없는 값이 나오기 때문에 샘플 평균도 하나의 확률 변수이다.
물론 이 확률 변수는 원래의 확률 변수와는 다른 분포를 갖는다.
확률 분포의 기대값¶
$$ \mu = \operatorname{E}[X] = \int_{-\infty}^{\infty} x f(x) dx $$$$ \mu = \operatorname{E}[X] = \sum xP(x) $$확률 변수의 pdf를 알고 있을 경우 다음과 같이 계산 하면 된다.
$$ \operatorname{E}[c] = c, \;\; (c는\;\; 상수)$$기대값의 성질
$$ \begin{align} \operatorname{E}[cX] &= c \operatorname{E}[X] \\ \operatorname{E}[X + Y] &= \operatorname{E}[X] + \operatorname{E}[Y] \end{align} $$선형성
$$ \text{E}\left[ (X-\mu_X)(Y-\mu_Y) \right] = 0 $$독립인 두 확률 변수(X, Y)의 기대값
$$ \operatorname{E}[ \bar{X} ] = \operatorname{E}[X] $$모평균과 표본 평균(샘플 평균)의 관계
표본 평균도 하나의 확률 변수이므로 샘플 평균에도 기대값이 존재한다.
또한 샘플 평균의 기댓값은 원래의 확률 변수의 기댓값과 일치함을 수학적으로 증명할 수 있다.
pf) $$ \begin{eqnarray} \operatorname{E}[\bar{X}] &=& \operatorname{E}\left[\dfrac{1}{N}\sum_{1}^{N}X_i \right] \\ &=& \dfrac{1}{N}\sum_{1}^{N}\operatorname{E}[X_i] \\ &=& \dfrac{1}{N}\sum_{1}^{N}\operatorname{E}[X] \\ &=& \dfrac{1}{N} N \operatorname{E}[X] \\ &=& \operatorname{E}[X] \\ \end{eqnarray} $$
중앙값(median)¶
중앙값(median)은 전체 자료를 크기별로 정렬하였을 때 가장 중앙에 위치하게 되는 값
median에도 sample median과 확률 분포로부터 계산한 이론적 median이 존재
계산
sample의 개수 = N $$ \begin{eqnarray*} \text{median} &=& \begin{cases} \frac{N+1}{2}의 \; 값 & \text{if}(N = 2k+1), \\ (\frac{N}{2}), (\frac{N}{2} + 1)의\; 평균\;\;\;\; & \text{if}(N = 2k) \end{cases} \end{eqnarray*} $$
여기서 F는 cdf 이다. $$ \text{median} = F^{-1}(0.5) $$$$ 0.5 = F(\text{median}) $$
최빈값(mode)¶
mode는 직역하면, 가장 빈번하게 나오는 값
하지만 연속 확률 분포인 경우에는 어느 값에 대해서나 특정한 값이 나올 확률은 0이다.
그러므로, 확률 밀도 함수의 값이 가장 큰 확률 변수의 값으로 정의한다.
- 즉, 확률 밀도 함수의 최대값의 위치이다.
- 다른 말로하면, 꼭지점!
수식 $$ \text{mode} = \arg \max_x f(x) $$
mode의 특징
- 이산(discrete) 샘플 자료에 대해서는 최빈값을 구할 수 있다.
- 연속(continuous) 샘플 자료는 최빈값이 존재하지 않거나 의미가 없다.
히스토그램을 그려서 구간을 분할하여 각 구간의 대표값으로 카테고리화하여 최빈값을 구해야 한다.
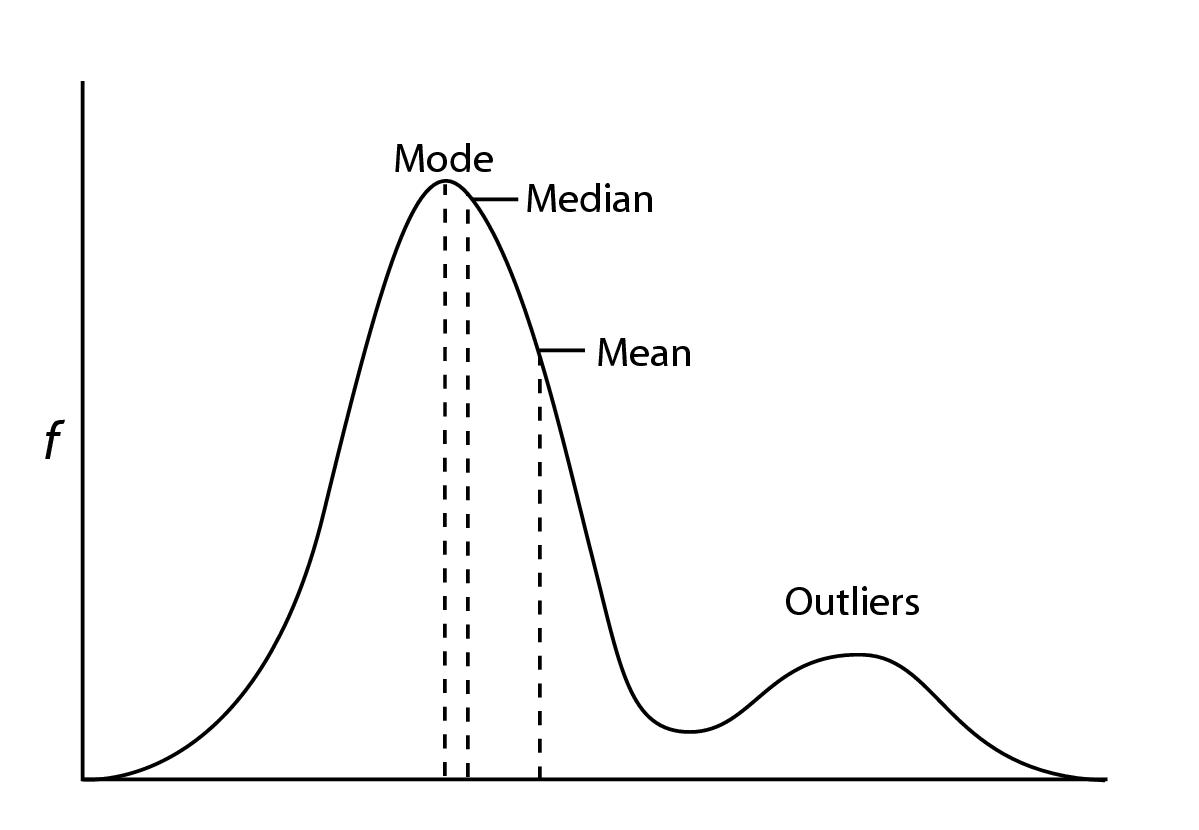
기댓값, 중앙값, 최빈값의 비교¶
확률 밀도 함수가 y축 대칭인 경우에는 기댓값, 중앙값, 최빈값이 모두 같다.
- ex) 가우시안 정규 분포
분포가 어느 한쪽으로 찌그러진(skewed) 경우
평균
- 가장 계산이 쉽다.
- outliner에 영향을 크게 받음.
중앙값
- 평균보다 계산량이 증가
- outliner에 대한 영향이 적음.
mode
- 최적화 과정을 통해서만 구할 수 있음. → 계산량이 가장 많으며, 오차가 크다.
- outliner에 대한 영향이 적음.
numpy를 활용하여 대표값을 구해보자.¶
import numpy as np
# 데이터 생성
np.random.seed(0)
x = np.random.normal(size=1000)
# 평균과 중앙값
np.mean(x), np.median(x)
# mode 구하기
## 연속형 변수 이므로 히스토그램을 그려야 한다.
### bins: [-10,10] 구간을 20개의 점을 찍어 19개 구간으로 나눈다.
### ns: 19개 구간안에 존재하는 x의 개수
ns, bins = np.histogram(x, bins=np.linspace(-10,10,20))
### 가장 값의 개수가 많은 구간을 선택 → mode
mode = np.argmax(ns)
bins[mode], bins[mode+1]
mode가 위치할 신뢰구간은 위와 같다.¶
# 결측치가 있는 데이터의 평균 구하기
a = np.array([[1, np.nan], [3, 4]])
a
np.nanmean(a)
# axis=0 : ↓ 연산
np.nanmean(a, axis=0)
# axis=1 : → 연산
np.nanmean(a, axis=1)
표본 분산(sample variance)¶
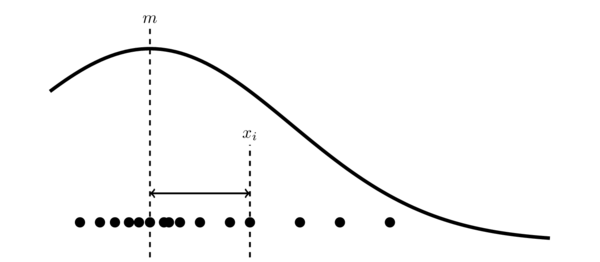
$$ s^2 = \dfrac{1}{N}\sum_{i=1}^{N} (x_i-m)^2 $$위의 그림에서 볼 수 있듯이 분산은 자료값과 평균 사이의 거리(편차)를 의미한다.
다만 자료값이 평균보다 작을 때는 음수가 나오므로 제곱을 하여 모두 양수로 만든 것이다.
$$ s^2_{\text{unbiased}} = \dfrac{1}{N-1}\sum_{i=1}^{N} (x_i-m)^2 $$위 식에서 구한 샘플 분산은 정확하게 말하면 편향 오차를 가진 편향 샘플 분산(biased sample variance)이다.
이와 대조되는 비편향 샘플 분산(unbiased sample variance)은 다음과 같이 구한다.
샘플 분산의 편향 오차에 대해서는 확률 분포의 분산과 같이 이후에 다룬다.
확률 분포의 분산¶
확률 변수의 확률 밀도 함수를 알고 있다면 다음과 같이 계산할 수 있다.
연속 확률 변수 $$ \sigma^2 = \text{Var}[X] = \text{E}[(X - \mu)^2] = \int_{-\infty}^{\infty} (x - \mu)^2 f(x)dx$$
이산 확률 변수 $$ \sigma^2 = \sum (x - \mu)^2 P(x)$$
분산의 성질¶
$$ \text{Var}[c] = 0 $$$$ \text{Var}[cX] = c^2 \cdot \text{Var}[X] $$분산은 다음과 같은 성질을 만족한다. $$ \text{Var}[X] \geq 0 $$
상수 c
$$ \text{Var}[X] = \text{E}[X^2] - (\text{E}[X])^2 = \text{E}[X^2] - \mu^2$$
Pf)
$$ \begin{eqnarray} \text{Var}[X] &=& \text{E}[(X - \mu)^2] \\ &=& \text{E}[X^2 - 2\mu X + \mu^2] \\ &=& \text{E}[X^2] - 2\mu\text{E}[X] + \mu^2 \\ &=& \text{E}[X^2] - 2\mu^2 + \mu^2 \\ &=& \text{E}[X^2] - \mu^2\\ \end{eqnarray} $$독립인 두 확률 변수의 분산¶
두 확률 변수 X, Y가 서로 독립이면 다음이 성립한다. $$ \text{Var}\left[ X + Y \right] = \text{Var}\left[ X \right] + \text{Var}\left[ Y \right]$$
Pf) $$ \begin{eqnarray} \text{Var}\left[ X + Y \right] &=& \text{E}\left[ (X + Y - (\mu_X + \mu_Y))^2 \right] \\ &=& \text{E}\left[ ((X -\mu_X) + (Y - \mu_Y))^2 \right] \\ &=& \text{E}\left[ (X -\mu_X)^2 + (Y - \mu_Y)^2 + 2(X-\mu_X)(Y-\mu_Y) \right] \\ &=& \text{E}\left[ (X -\mu_X)^2 \right] + \text{E}\left[ (Y - \mu_Y)^2 \right] + 2\text{E}\left[ (X-\mu_X)(Y-\mu_Y) \right] \\ &=& \text{E}\left[ (X -\mu_X)^2 \right] + \text{E}\left[ (Y - \mu_Y)^2 \right] \end{eqnarray} $$
샘플 평균의 분산¶
$$ \text{E}[\bar{X}] = \text{E}[{X}]$$확률 변수 X의 표본 평균도 일종의 확률 변수이며, 표본 평균의 기대값은 원래 확률 변수 X의 기대값과 일치한다는 것을 알고 있다.
$$ \text{E}\left[ (X_i-\mu)(X_j-\mu) \right] = 0, \;\;\; (\text{ if i $\neq$ j}) $$그렇다면, 표본 평균의 분산과 원래 확률 변수 X의 분산은 어떨까?
- 먼저, 개별 sample에 대한 확률 변수 Xi는 서로 독립이라고 가정하자. 그러면 다음이 성립한다.
- 또한, 개별 sample에 대한 확률 변수 Xi의 기대값과 분산은 원래 확률 변수 X와 같다고 하자.
$$ \text{Var}[\bar{X}] \;=\; \dfrac{\sigma^2}{N} $$이때, 표본 평균의 분산과 모집단의 분산의 관계를 알아보자.
Pf) $$ \begin{eqnarray} \text{Var}[\bar{X}] &=& \text{E} \left[ \left( \bar{X} - \mu \right)^2 \right] \\ &=& \text{E} \left[ \left( \dfrac{1}{N} \sum_{i=1}^N X_i - \mu \right)^2 \right] \\ &=& \text{E} \left[ \left( \sum_{i=1}^N \left( \dfrac{1}{N} X_i - \dfrac{1}{N}\mu \right) \right)^2 \right] \\ &=& \text{E} \left[ \left( \dfrac{1}{N} \sum_{i=1}^N (X_i - \mu) \right)^2 \right] \\ &=& \text{E} \left[ \dfrac{1}{N^2} \sum_{i=1}^N \sum_{j=1}^N (X_i - \mu) (X_j - \mu) \right] \\ &=& \text{E} \left[ \dfrac{1}{N^2} \sum_{i=1}^N (X_i - \mu)^2 \right] \\ &=& \frac{1}{N^2} \sum_{i=1}^N (\text{E}(X_{i}^2) -2\mu\text{E}(X_{i}) + \mu^2) \\ &=& \frac{1}{N^2} \sum_{i=1}^N (\text{E}(X_{i}^2) -\mu^2) \\ &=& \frac{1}{N^2} \sum_{i=1}^N (\sigma^2) \\ &=& \dfrac{1}{N^2} N\cdot\sigma^2 \\ &=& \dfrac{\sigma^2}{N} \end{eqnarray} $$
표본 분산(sample variance)의 기대값이 모집단의 분산과 같아지려면?¶
둘 중 무엇을 사용해야 할까?
- biased sample variance
- unbiased sample variance
$$ \begin{eqnarray} \text{E} \left[ { \dfrac{1}{N} \sum_{i=1}^N (X_i -\mu)(\bar{X} - \mu) } \right] &=& \text{E} \left[ { \dfrac{1}{N} \sum_{i=1}^N (X_i -\mu) \left( \dfrac{1}{N} \sum_{j=1}^N X_j - \mu \right) } \right] \\ &=& \text{E} \left[ { \dfrac{1}{N} \sum_{i=1}^N (X_i -\mu) \left( \dfrac{1}{N} \sum_{j=1}^N ( X_j - \mu ) \right) } \right] \\ &=& \text{E} \left[ { \dfrac{1}{N^2} \sum_{i=1}^N \sum_{j=1}^N (X_i -\mu) ( X_j - \mu )} \right] \\ &=& \text{E} \left[ { \dfrac{1}{N^2} \sum_{i=1}^N (X_i -\mu)^2 }\right] \\ &=& \dfrac{1}{N} \text{Var}[X] = \dfrac{\sigma^2}{N} \end{eqnarray} $$여기서
$$ \text{E}[s^2] = \sigma^2 - \dfrac{2\sigma^2}{N} + \dfrac{\sigma^2}{N} = \dfrac{N-1}{N}\sigma^2 $$따라서 본래 식으로 돌아가면
그러므로 샘플 분산의 기대값이 정확하게 모분산이 되려면 N-1로 나눠줘야 한다.¶
$$ \begin{eqnarray} \sigma^2 &=& \dfrac{N}{N-1} \text{E}[s^2] \\ &=& \dfrac{N}{N-1} \text{E} \left[ \dfrac{1}{N} \sum (X_i-\bar{X})^2 \right] \\ &=& \text{E} \left[ \dfrac{1}{N-1} \sum (X_i-\bar{X})^2 \right] \\ &=& \text{E} \left[ s^2_{\text{unbiased}} \right] \\ \end{eqnarray} $$unbiased sample variance¶
$$ s^2_{\text{unbiased}} = \dfrac{1}{N-1} \sum (X_i-\bar{X})^2 $$#scipy와 seaborn은 항상 같이 import 하도록 하자.
import scipy as sp
import seaborn as sns
sp.random.seed(0)
x = sp.stats.norm(0, 2).rvs(1000) # mean=0, standard deviation=2
len(x)
np.var(x)
# unbiased variance
## N - ddof
np.var(x, ddof=1)