11 Sep 2017 » probability, statistics
2017-09-11-probability_2

수식이 깨질 경우 새로고침을 눌러주세요.

Probability for Data-Science-14

다변수 확률 모형 ③

  • Categorical (Multinoulli)
  • Multinomial
  • Dirichlet
  • ✓Multivariate Gaussian Normal

Multivariate Gaussian Normal(다변량 가우시안 정규 분포)

다변량 가우시안 정규 분포 혹은 간단히 다변량 정규 분포(MVN: Multivariate Normal)라고 한다.

복수의 확률 변수를 모형화하는데 가장 많이 사용되는 분포이다.

$$ D차원\;\; 다변수\;\; 정규\;\; 분포의\;\; 확률\; 밀도\; 함수는\;\; 평균\; 벡터( \mu)와\;\; 공분산\; 행렬(\Sigma)라는\;\; 두\;\; 개의\;\; 모수를\;\; 갖는다.\\ \\다음과\;\; 같은\;\; 수식으로\;\; 정의된다.\;\; 이\;\; 때\;\; 공분산\;\; 행렬은\;\; 역행렬이\;\; 존재하는\;\; 대칭\;\; 행렬이어야\;\; 한다. $$$$ \mathcal{N}(x ; \mu, \Sigma) = \dfrac{1}{(2\pi)^{D/2} |\Sigma| ^{1/2}} \exp \left( -\dfrac{1}{2} (x-\mu)^T \Sigma^{-1} (x-\mu) \right) $$

이 식에서 각 기호의 의미는 다음과 같다.

$$ x \in \mathbf{R}^D : \;\;\;\; 확률\; 변수\; 벡터 \\ \mu \in \mathbf{R}^D : \;\;\;\; 평균\; 벡터 \\ \Sigma \in \mathbf{R}^{D\times D} : \;\;\;\; 공분산\; 벡터 \\ \Sigma^{-1} \in \mathbf{R}^{D\times D} : \;\;\;\; 공분산\; 벡터의\; 역행렬 \\ |\Sigma| : \;\;\;\;\Sigma의\; 디터미넌트 = 스칼라\; 값 $$

공분산 벡터의 역행렬 $\Sigma^{-1}$는 precision matrix 혹은 concentration matrix 라고도 한다.

scipy를 사용하여 다변수 정규 분포를 더 알아 보자.

SciPy의 stats 서브패키지에는 다변수 정규 분포를 위한 multivariate_normal 클래스가 있다.

mean 인수로 평균 벡터를, cov 인수로 공분산 행렬을 받는다.

2차원 다변수 정규 분포의 예를 몇가지 살펴보자.

$$ x = \begin{bmatrix}x_1 \\ x_2 \end{bmatrix} $$

Case_1

$$만약 \;\;\;\; \mu = \begin{bmatrix}2 \\ 3 \end{bmatrix}, \;\;\; \Sigma = \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix} 이면, $$
$$ | \Sigma| = 1, \;\;\; \Sigma^{-1} = \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix} $$$$ (x-\mu)^T \Sigma^{-1} (x-\mu) = \begin{bmatrix}x_1 - 2 & x_2 - 3 \end{bmatrix} \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix}x_1 - 2 \\ x_2 - 3 \end{bmatrix} = (x_1 - 2)^2 + (x_2 - 3)^2 $$$$ \mathcal{N}(x_1, x_2) = \dfrac{1}{2\pi} \exp \left( -\dfrac{1}{2} \left( (x_1 - 2)^2 + (x_2 - 3)^2 \right) \right) $$

이 확률 밀도 함수의 모양은 다음과 같다.

In [1]:
# -*- coding: utf-8 -*-

import seaborn as sns
import pandas as pd
import scipy as sp
import matplotlib as mpl
import matplotlib.pylab as plt
import numpy as np
%matplotlib inline
In [2]:
mu = [2, 3]
cov = [[1, 0], [0, 1]]
rv = sp.stats.multivariate_normal(mu, cov)

xx = np.linspace(0, 4, 120)
yy = np.linspace(1, 5, 150)

## xx, yy 같은 shape의 벡터 → XX, YY 서로 같은 매트릭스로 변환
# meshgrid : 벡터를 행렬로 변환
XX, YY = np.meshgrid(xx, yy)

plt.grid(False)
plt.contourf(XX, YY, rv.pdf(np.dstack([XX, YY])))
plt.axis("equal")
plt.show()

찌그러진 정도가 적을수록( 원에 가까울 수록) → 상관계수 = 0

Case_2

$$ 만약,\;\;\;\; \mu = \begin{bmatrix}2 \\ 3 \end{bmatrix}, \;\;\; \Sigma = \begin{bmatrix}2 & 3 \\ 3 & 7 \end{bmatrix} 이면, $$$$ |\Sigma| = 5,\;\;\; \Sigma^{-1} = \begin{bmatrix}1.4 & -0.6 \\ -0.6 & 0.4 \end{bmatrix} $$$$ (x-\mu)^T \Sigma^{-1} (x-\mu) = \begin{bmatrix}x_1 - 2 & x_2 - 3 \end{bmatrix} \begin{bmatrix}1.4 & -0.6 \\ -0.6 & 0.4\end{bmatrix} \begin{bmatrix}x_1 - 2 \\ x_2 - 3 \end{bmatrix} = \dfrac{1}{10}\left(14(x_1 - 2)^2 - 12(x_1 - 2)(x_2 - 3) + 4(x_2 - 3)^2\right) $$$$ \mathcal{N}(x_1, x_2) = \dfrac{1}{20\pi} \exp \left( -\dfrac{1}{10}\left(7(x_1 - 2)^2 - 6(x_1 - 2)(x_2 - 3) + 2(x_2 - 3)^2\right) \right) $$

이 확률 밀도 함수의 모양은 다음과 같다.

In [3]:
mu = [2, 3]
cov = [[2, 3],[3, 7]]
rv = sp.stats.multivariate_normal(mu, cov)
xx = np.linspace(0, 4, 120)
yy = np.linspace(1, 5, 150)

## xx, yy 같은 shape의 벡터 → XX, YY 서로 같은 매트릭스로 변환
# meshgrid : 벡터를 행렬로 변환
XX, YY = np.meshgrid(xx, yy)
plt.grid(False)
plt.contourf(XX, YY, rv.pdf(np.dstack([XX, YY])))
plt.axis("equal")
plt.show()

찌그러진 정도가 클수록 → 상관계수 = 1

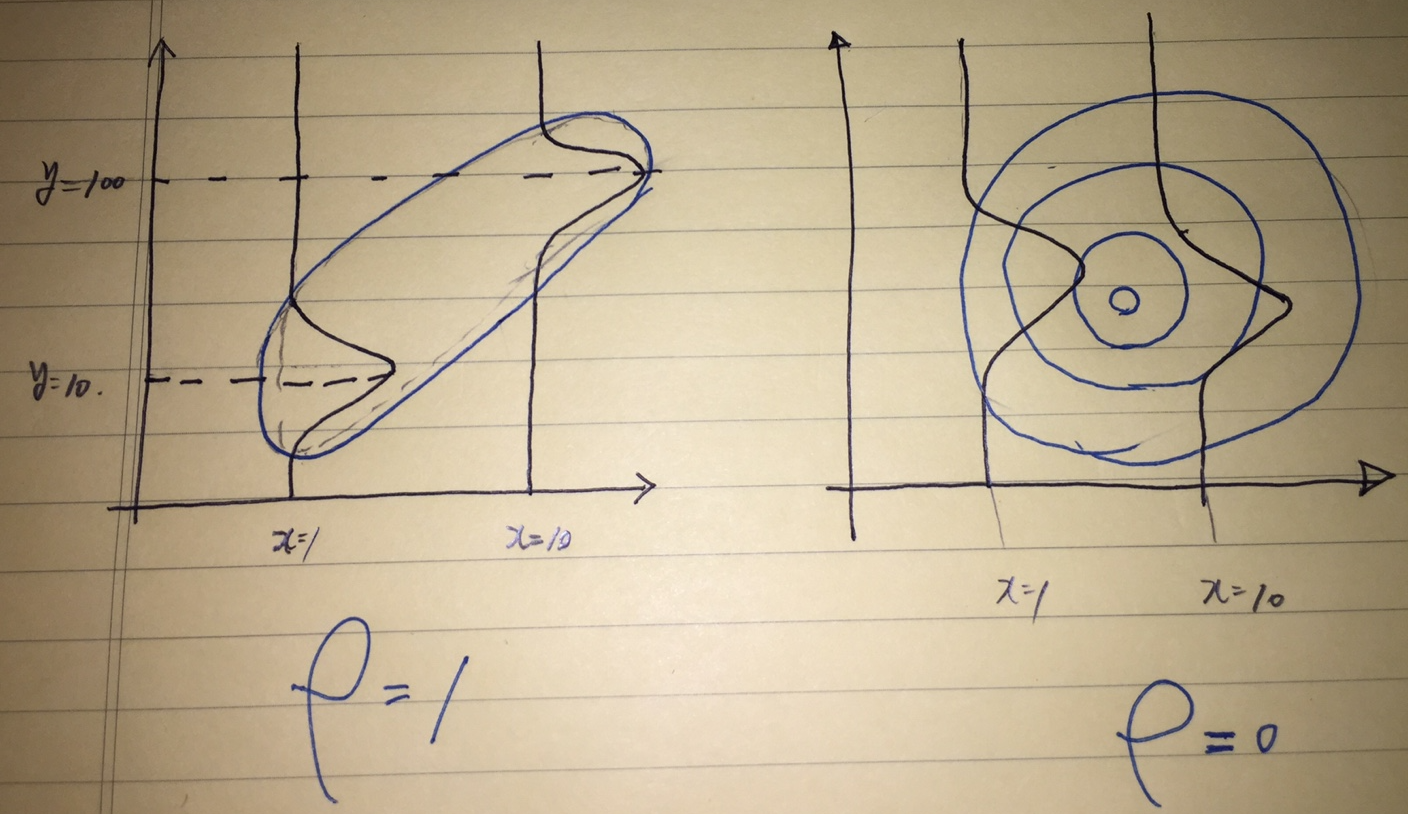
찌그러진 정도가 적을수록( 원에 가까울 수록) → 상관계수 = 0

찌그러진 정도가 클수록 → 상관계수 = 1

다변수 정규 분포의 최적화

다변수 정규 분포를 모수에 대해 최적화하는 문제를 풀어보자.

  • 어떤 함수에 로그를 취해도 최고점이나 최저점의 위치는 변하지 않는다.

다만, 폭이 좁아지고, 높이는 높아진다.

또한, 아래에서 보듯이 계산량이 줄어들기 때문에 로그를 취한 분포함수를 최적화를 한다.

Log Gaussian Normal

$$ \log N(x|\mu, \Sigma) = -\dfrac{1}{2} \log|\Sigma| - \dfrac{1}{2} (x-\mu)^T \Sigma^{-1} (x-\mu) $$

precision matrix $ \Lambda = \Sigma ^{-1} $

$$ \log N(x|\mu, \Sigma) = \dfrac{1}{2} \log|\Lambda| - \dfrac{1}{2} (x-\mu)^T \Lambda (x-\mu) $$
$$ \mathcal{N}(x ; \mu, \Sigma) = \dfrac{1}{(2\pi)^{D/2} |\Sigma| ^{1/2}} \exp \left( -\dfrac{1}{2} (x-\mu)^T \Sigma^{-1} (x-\mu) \right) $$$$ \log \mathcal{N}(x; \mu, \Sigma) = -\dfrac{D}{2}\log{2\pi} -\dfrac{1}{2} \log|\Sigma| - \dfrac{1}{2} (x-\mu)^T \Sigma^{-1} (x-\mu) $$$$ 여기에서\; 기호를\; 단순하게\; 하기\; 위해\; precision\; matrix\; \Sigma ^{-1} 를\; \Lambda 로\; 표시하고\; 미분할\; 때\; 없어지는\; 상수항을\; 제외한\; 부분을\; 함수\; f로\; 나타내자. $$$$ f = \log| \Lambda| - (x-\mu)^T \Lambda (x-\mu) $$
$$ 스칼라\;\; 함수\;\; f를\;\; 평균\;\; 벡터 \mu로\;\; 미분하면\;\; 다음과\;\; 같다. $$$$ \begin{eqnarray} \dfrac{\partial f}{\partial \mu} &=& \dfrac{\partial}{\partial \mu} \big( \log | \Lambda| \big) - \dfrac{\partial}{\partial \mu} \big( (x-\mu)^T \Lambda (x-\mu) \big) \\ &=& -(\Lambda + \Lambda^T)(x-\mu) \\ &=& 0 \end{eqnarray} $$$$ \therefore \;\; \mu = x $$

위 함수를 미분하면 다음 변수에서 최적화가 된다.

$$ \mu = \dfrac{1}{N}\sum_{i=1}^N x_i $$$$ \Sigma = \dfrac{1}{N}\sum_{i=1}^N (x_i-\mu)(x_i-\mu)^T $$

$$ 이번에는\; 두\; 개의\; 다변수\; 정규\; 분포\; 확률\; 변수\; X,\; Y가\; 있을\; 경우를\; 생각해\; 보자.\; 두\; 확률\; 변수가\; 독립이며\; 모수\; \mu,\; \Lambda가\; 같다고\; 가정하자. $$$$ \\이\; 때\; 로그\; 정규\; 분포는\; 다음과\; 같다. $$$$ \begin{eqnarray} f &=& \log \left( \mathcal{N}(x; \mu, \Sigma)\mathcal{N}(y; \mu, \Sigma)\right) \\ &=& \log \mathcal{N}(x; \mu, \Sigma) + \log \mathcal{N}(y; \mu, \Sigma) \\ &=& - \log|\Sigma| - \dfrac{1}{2} (x-\mu)^T \Lambda (x-\mu) - \dfrac{1}{2} (y-\mu)^T \Lambda (y-\mu) \end{eqnarray} $$
$$ 이\; 함수\; f를\; 평균\; 벡터\; \mu와\; precision\; matrix \;\Lambda 로\; 미분하면\; 다음과\; 같다. $$$$ \begin{eqnarray} 2\cdot\dfrac{\partial f}{\partial \mu} &=& \dfrac{\partial}{\partial \mu} \big( 2\log | \Lambda | \big) - \dfrac{\partial}{\partial \mu} \big( (x-\mu)^T \Lambda (x-\mu) \big) - \dfrac{\partial}{\partial \mu} \big( (y-\mu)^T \Lambda (y-\mu) \big) \\ &=& - (\Lambda + \Lambda^T)(x-\mu) - (\Lambda + \Lambda^T)(y-\mu) \\ &=& 0 \end{eqnarray} $$$$ \therefore \;\; \mu = \dfrac{x + y}{2} $$$$ \begin{eqnarray} 2\cdot\dfrac{\partial f}{\partial \Lambda} &=& \dfrac{\partial}{\partial \Lambda} \big( 2\log | \Lambda| \big) - \dfrac{\partial}{\partial \Lambda} \big( (x-\mu)^T \Lambda (x-\mu) \big) - \dfrac{\partial}{\partial \Lambda} \big( (y-\mu)^T \Lambda (y-\mu) \big) \\ &=& (2\Lambda^{-1})^T - \dfrac{\partial}{\partial \Lambda} \left( \text{tr} \left( (x-\mu)(x-\mu)^T \Lambda \right) \right) - \dfrac{\partial}{\partial \Lambda} \left( \text{tr} \left( (y-\mu)(y-\mu)^T \Lambda \right) \right) \\ &=& 2\Sigma^T - ((x-\mu)(x-\mu)^T)^T - ((y-\mu)(y-\mu)^T)^T \\ &=& 0 \end{eqnarray} $$$$ \therefore \;\; \Sigma = \dfrac{1}{2} \left( (x-\mu)(x-\mu)^T + (y-\mu)(y-\mu)^T \right) $$

다변량 가우시안 정규분포를 좀 더 그려 보자.

In [4]:
from scipy.stats import multivariate_normal
XX, YY = np.mgrid[-5:5:500j, -2:2:200j]
rv = multivariate_normal([0.5, -0.2], [[2.0, 0.3], [0.3, 0.5]])
plt.grid(False)
plt.contour(XX, YY, rv.pdf(np.dstack((XX, YY))))
Out[4]:
<matplotlib.contour.QuadContourSet at 0x10df15c88>
In [5]:
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(XX, YY, rv.pdf(np.dstack((XX, YY))))
Out[5]:
<mpl_toolkits.mplot3d.art3d.Poly3DCollection at 0x10e66bba8>

Partitioned Multivariate Gaussian

Linear Discriminant Analyis 때 활용

$$ x = \begin{bmatrix} x_a \\ x_b \end{bmatrix} ,\;\; \mu = \begin{bmatrix} \mu_a \\ \mu_b \end{bmatrix} ,\;\; \Sigma = \begin{bmatrix} \Sigma_{aa} & \Sigma_{ab} \\ \Sigma_{ba} & \Sigma_{bb} \end{bmatrix} ,\;\; \Lambda = \begin{bmatrix} \Lambda_{aa} & \Lambda_{ab} \\ \Lambda_{ba} & \Lambda_{bb} \end{bmatrix} $$
  • Conditional distribution:
$$ p(x_a | x_b ) = N(x|\mu_{a|b} , \Lambda_{aa}^{−1}) $$$$ \mu_{a|b} = \mu_a - \Lambda_{aa}^{−1}\Lambda_{ab} (x_b - \mu_b) $$
  • Marginal distribution:
$$ p(x_a) = N(x_a|\mu_a , \Sigma_{aa}) $$

Chain Rule

$$ X_N \leftrightarrow^{\text{dependent}} \theta \leftrightarrow^{\text{dependent}} X_{N-1} $$

$$ X_N \leftrightarrow^{\text{independent}} X_{N-1} $$

$$ P(X_N, X_{N-1}|\theta) = P(X_N|\theta) \cdot P(X_{N-1}|\theta) $$

Chain Rule $$ P(X_{1:N}|\theta) = P(X_1|\theta) P(X_2|X_1, \theta) \cdots P(X_N|X_{1:N-1},\theta) = \prod_{i=1}^N P(X_i|\theta) $$

  • likelyhood를 구할 때 주로 사용한다.
$$ x_i는\; 서로\; 독립이므로\; 아래가\; 성립한다. $$$$ \begin{eqnarray} P(X_{1:N}|\theta) &=& P(X_1,X_2,X_3,\cdots,X_N|\theta) \\ &=& P(X_2,X_3,\cdots,X_N|\theta)\cdot P(X_1, \theta) \\ &=& P(X_3,\cdots,X_N|\theta)\cdot P(X_2, \theta)\cdot P(X_1, \theta) \\ &=& \vdots \\ &=& P(X_N|\theta)\cdot P(X_N-1|\theta)\cdots\cdot P(X_2, \theta)\cdot P(X_1, \theta) \\ &=& \prod_{i=1}^N P(X_i|\theta) \end{eqnarray} $$

Related Posts