수식이 깨질 경우 새로고침을 눌러주세요.
가설과 검정 ②¶
검정 방법¶
검정을 어떻게 할 것인가?
분포의 파라미터 값이 특정한 값임을 어떻게 보일 것인가?
검정 통계량(Test Statistics)
일반적인 검정 방법은 다음과 같다.¶
- 모수 값이 특정한 조건을 만족한다면 해당 확률 변수로부터 만들어진 표본(sample) 데이터들은 어떤 규칙을 따르게 된다.
- 표본(데이터 집합)에서 어떤 규칙에 따라 값을 구하면 그 값은 특정한 확률 분포를 따르게 된다. 이 값을 검정 통계량(test statistics)라고 한다.
- 검정통계량이 따르는 확률 분포를 검정 통계 분포(test statistics distribution)라고 한다.
- 검정 통계 분포의 종류 및 모수의 값은 처음에 정한 가설(귀무 가설)에 의해 결정된다.
- 만약 유의 확률이 미리 정한 특정한 기준값보다 작은 경우를 생각하자.
- 이 기준값을 유의 수준(significance level)이라고 하는 데 보통 1% 혹은 5% 정도의 작은 값을 지정한다.
- 유의 확률이 유의 수준보다도 작다는 말은 해당 검정 통계 분포에서 이 검정 통계치가 나올 수 있는 확률이 아주 작다는 의미이다.
- 즉, 귀무 가설이 틀렸다는 의미이다. 따라서 이 경우, 귀무 가설을 기각(reject)한다.
- 만약 유의 확률이 유의 수준보다 크다면
- 검정 통계 분포에서 이 검정 통계량이 나오는 것이 불가능하지만은 않다는 의미이므로 귀무 가설을 기각할 수 없다.
- 따라서, 이 경우에는 귀무 가설을 채택(accept)한다.
검정 통계량¶
$$\bbox[7px, border:2px solid blue]{ \theta → \alpha} $$원래의 확률 변수와 관련이 있는 새로운 확률 변수
가설 검정에서 증명하고자 하는 원래 확률 변수의 확률 분모 파라미터(theta)의 값에 의해 검정 통계량 분포의 파라미터(alpha)가 결정된다.
그렇다면, 검정 통계량은 무엇일까?
- 검정을 하려면 즉, 귀무 가설이 맞거나 틀린 것을 증명하려면 어떤 증거가 있어야 한다. 이 증거가 검정 통계량(test statistics)이다.
예를 들어 이해해보자.
- 환자가 "어떤 병에 걸렸다"라는 가설을 증명하려면 환자의 혈액을 채취하여 혈액 내 특정한 성분의 수치를 측정해야 한다.
- 이 때 혈액 내 특정한 성분의 수치가 검정 통계량이 된다.
- "어떤 학생이 우등상을 받을 것이다."라는 가설을 증명하려면 시험 성적을 알아내면 된다.
- 이 때, 시험 성적이 검정 통계량이다.
$$ \text{Test Statistics(검정 통계량) } $$$$ T = f(x_1, x_2, \ldots, x_n) $$수식
- 검정 통계량은 아래처럼 확률변수에 관한 수식으로 표현할 수 있다.
검정 통계량의 예¶
$$ \bbox[8px, border:2px solid red]{검정통계량\; T = \dfrac{m}{s/\sqrt{N}}} \\ \\단,\;\; m = \dfrac{1}{N}\sum_{i=1}^{N} x_i,\;\;\;\; s^2 = \dfrac{1}{N}\sum_{i=1}^{N} (x_i-m)^2\; 이다. $$sum(합)
- 동전을 던져서 앞면이 나온 횟수(Bernoulli 분포의 sample의 합)
- 정규 분포의 sample의 합
수익률 ~ N(평균, 분산) $$ N\text{개의 수익률 데이터}\;\; x_1, \cdots, x_N \text{에서 다음 수식으로 계산한 값도 검정 통계량이 된다.} $$
sum of squared(제곱의 합)
- 분산 및 표준편차 검정에 사용
ratio of sums(두 sample 집합의 합의 비율)
- 두 랜덤 변수의 파라미터 비교에 사용
검정 통계량에 대해 좀 더 이해해보자.¶
$$\text{따라서 검정 통계량}\;\; t\; \text{도 검정 통계량 확률 변수}\;\; T\;\text{라는 확률 변수의 표본으로 볼 수 있다.}$$검정 통계량은 표본 자료에서 계산된 함수값이므로 표본처럼 확률적(random)이다.
즉, 경우에 따라 표본 값이 달라질 수 있는 것처럼 달라진 표본값에 의해 검정 통계량도 달라진다.
또한, 어떤 귀무 가설을 만족하는 표본을 입력 변수로 놓고 특정한 함수로 계산한 검정 통계량이 특정한 분포를 따른다는 것을 수학적인 증명을 통해 보여야 한다.
통계학자들의 중요한 업적 중의 하나가 특정한 귀무 가설에 대해 어떤 검정 통계량 함수가 어떤 검정 통계량 분포를 따른 다는 것을 증명한 것이다.
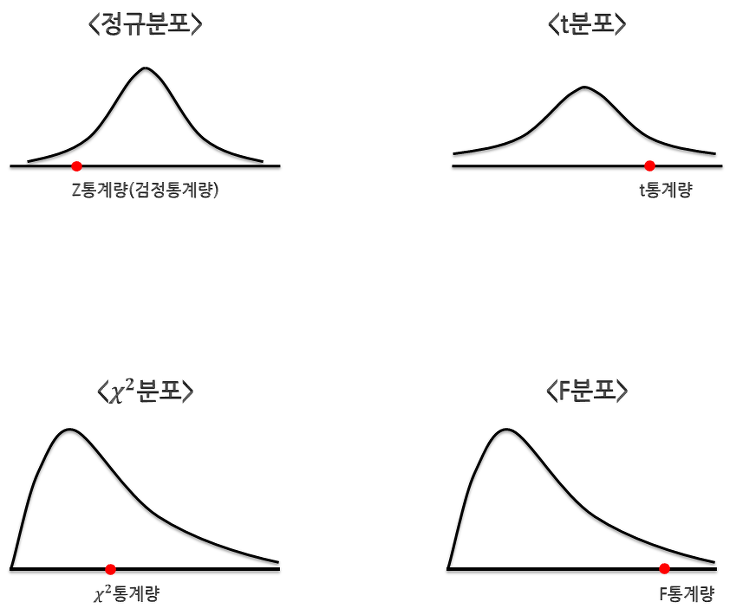
다음 도식을 보고 기억해 두자.¶
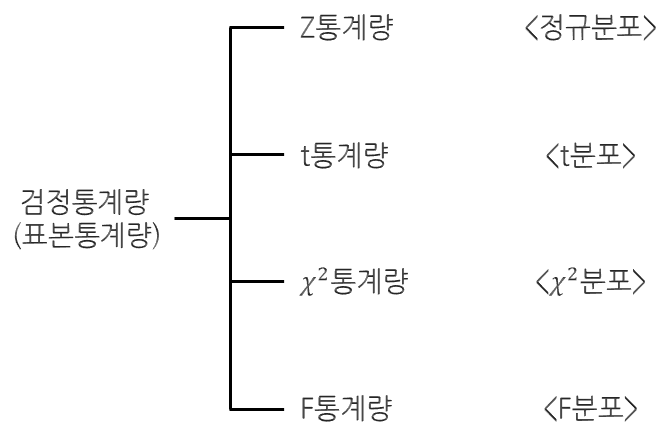
일반적으로 많이 사용되는 검정 통계량에 대해 알아 보자.¶
1. 베르누이 분포 확률 변수¶
$$ x \sim Bern(\theta) \;\; \rightarrow \;\; t = \sum x \sim Bin(N, \theta) $$모수 theta를 가지는 베르누이 분포 확률 변수에 대해서는 전체 시도 횟수 N 번 중 성공한 횟수 n 자체를 검정 통계량으로 쓸 수 있다.
이 검정 통계량은 자유도 (N) 과 모수 theta를 가지는 이항 분포를 따른다.
2. 카테고리 분포 확률 변수¶
$$ X \sim Cat(X;\boldsymbol\alpha) \;\; \rightarrow \;\; t = \sum x \sim Mul(X; N, \boldsymbol\alpha) $$모수 벡터 alpha를 가지는 카테고리 분포 확률 변수에 대해서는 전체 시도 횟수 N 번 중 성공한 횟수 벡터 X 자체를 검정 통계량으로 쓸 수 있다.
이 검정 통계량은 자유도 N과 모수 벡터 alpha를 가지는 다항 분포를 따른다.
3. 모수의 분산을 알고 있는 정규 분포 확률 변수¶
$$ x \sim \mathcal{N}(\mu, \sigma^2) \;\; \rightarrow \;\; z = \dfrac{\bar{x}-\mu}{\sigma \;/\sqrt{N}} \sim \mathcal{N}(0,1) $$$$ \text{여기에서 }\;\;\;\bar{x} = \dfrac{1}{N}\sum_{i=1}^{N} x_i $$모수의 분산을 알고 있는 정규 분포 확률 변수에 대해서는 다음과 같이 샘플 평균을 정규화(nomarlize)한 값을 검정 통계량으로 쓴다.
이 검정 통계량은 표준 정규 분포를 따른다. 이 검정 통계량은 특별히 z라고 부른다.
4. 모수의 분산을 모르는 정규 분포 확률 변수¶
평균 모수에 대한 검정을 할 때는 다음과 같이 샘플 평균을 샘플 분산으로 정규화(nomarlize)한 값을 검정 통계량으로 쓴다.
이 검정 통계량은 자유도가 (N-1)인 표준 student-t 분포를 따른다. (N) 은 데이터의 개수이다.
$$ x \sim \mathcal{N}(\mu, \sigma^2) \;\; \rightarrow \;\; t = (N-1)\dfrac{s^2}{\sigma^2} \sim \chi^2 (t;N-1) $$분산 모수에 대한 검정을 할 때는 다음과 같이 샘플 분산을 정규화(normalize)한 값을 검정 통계량으로 쓴다.
이 검정 통계량은 자유도가 N-1 인 카이 제곱 분포를 따른다. N 은 데이터의 개수이다.
5. 기타 검정 통계량 확률 모형¶
chi-squared
- 정규 분포의 샘플 집합의 제곱의 합은 chi-squared 분포 $$ x \sim N \;\; \rightarrow \;\; \sum x^2 \sim \chi^2(N) $$
F
두 chi-squared 분포의 샘플의 (정규화된) 비율은 F 분포 $$ x_1, x_2 \sim \chi^2 \;\; \rightarrow \;\; \dfrac{x_1/s_1}{x_2/s_2} \sim F(n_1,\; n_2) $$
student-t 분포의 샘플의 제곱은 F 분포 $$ x \sim t \;\; \rightarrow \;\; x^2 \sim F $$
유의 확률 p-value¶
귀무 가설이 사실이라는 가정하에 검정 통계량이 따르는 검정 통계량 분포를 알고 있다면
실제 데이터에서 계산한 검정 통계량 숫자가 분포에서 어느 부분쯤에 위치해 있는지를 알 수 있다.
이 위치를 나타내는 값이 바로 유의 확률(p-value) 이다.
검정 통계량의 유의 확률(p-value)¶
검정 통계량 숫자보다 더 희귀한(rare) 값이면서 대립 가설을 따르는 값이 나올 수 있는 확률을 말한다.
이 확률은 검정 통계 확률 분포 밀도 함수(pdf)에서 양 끝의 꼬리(tail)부분에 해당하는 영역의 면적으로 계산한다.
실제로는 누적 확률 분포 함수를 사용한다.
P-value는 항상 헷갈린다! 뜬 구름 잡는 소리하지 말고 다음을 보고 이해하고 기억하자!¶
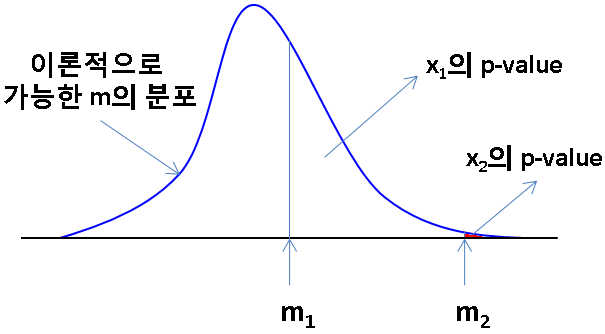
위 분포는 귀무가설이 참이라고 가정하고, 그 가설을 바탕으로 그린 이론적 분포이다.¶
기억하자. p-value는 귀무 가설을 지지하는 확률이다.
이 때, 주어진 자료를 바탕으로 m_1이라는 평균(검정 통계량)을 구했다.
- m_1의 p-value가 크다 → 귀무가설을 기각할 수 없으므로, 일단은 채택(맞는지는 불확실하나 대안이 없으므로 채택)
또한, 주어진 자료를 바탕으로 m_2라는 평균(검정 통계량)을 구했다.
- m_2의 p-value가 매우 작다. → 저 이론적 분포를 가져온 가설(귀무 가설)이 잘못되었다고 판단 → 귀무가설 기각 / 대립가설 채택
위의 예로 P-value(유의 확률)의 개념을 잡았을 것이다.¶
P-value의 개념을 간단히 다시 정리해보자.¶
p-value는 귀무가설(null hypothesis, H0) 이 맞다는 전제 하에, 검정 통계량(statistics)이 실제로 관측된 값 이상일 확률이다.
검정 통계량(statistics)이란 분포로부터 계산되는 값을 말하는데, 흔히 평균 / 평균의 차이 / 분산 / nth moment 등이 있을 수 있다.
p-value는 귀무가설을 지지하는 확률
- p-value가 작으면 귀무가설이 틀렸다고 여기고, 기각하고 대립가설을 채택함.
- p-value는 현재 구한 통계값이 얼마나 자주 나올 것인가를 의미하기도 한다.
- 가설검정은 전체 데이터를 갖고 하는 것이 아닌 sampling 된 데이터를 갖고 하는 것이다. 그래서 p-value가 필요함
머리가 아프겠지만 P-value(유의 확률)에 대한 오해를 바로 잡고 좀 더 깊이 이해해보자.¶
p-value는 귀무가설이 참일 확률이 아니다.¶
p-value는 귀무가설을 지지하는 확률이다. (귀무 가설 하에 표본의 분포를 그리고 그 분포와 모분포(실제 이상적인 분포)를 비교할 수 있는 확률이다.)
귀무가설이 참일 확률은 구할 수 없다.
p-value가 낮아도 귀무가설이 참일 수 있고, p-value가 (아주) 높아도 귀무가설은 틀릴 수 있다.
p-value와 유의수준(alpha)을 통해 귀무가설을 기각했는데, 이게 올바른 판단인 것인가?¶
안타깝게도 귀무가설을 잘못 기각했는지, 아니면 맞게 기각했는지는 확인할 수 없다.
즉, 귀무 가설을 잘못 기각했다는 것은 확률값으로 판단할 수가 없다.
귀무가설이 맞다는 전제 하에 나온 분포에서 확률을 보는 것이다.
- 만약 이 분포에서 p-value = 0.001의 값을 얻었고, 낮은 유의확률을 갖기 때문에 귀무가설을 기각했다.
- 하지만, 우리는 귀무가설이 맞았음에도 불구하고 p-value가 낮았기 때문에 기각했다고 말할 수는 없다.
- 왜냐하면, 0.1%의 경우에 대해서 귀무 가설이 참인지 거짓인지 확인할 방법이 없기 때문이다.
그리고 정의상 p-value는 그런 개념이 아니다. 만약 애초에 귀무가설이 틀렸다고 해보자.
- 그런 상황에서도 여전히 p-value는 구해지는데, 그런 p-value가 과연 귀무가설을 잘못 기각한 확률이 될 수 있을까?
- 애초부터 귀무가설이 틀릴 수도 있고, 귀무가설이 거짓이라도 p-value는 여전히 구해지기 때문에 귀무 가설이 참인지 거짓인지는 확인할 수가 없다.
- 그래서 우리는 귀무가설이 맞다고 가정하고 문제를 풀기 시작하는 것이다.
일반적으로 p-value는 어떤 가설을 전제로, 그 가설이 맞는다는 가정 하에, 내가 현재 구한 통계값이 얼마나 자주 나올 것인가를 의미한다고 할 수 있다.¶
가설검정은 전체 데이터를 갖고 하는 것이 아닌 sampling 된 데이터를 갖고 하는 것이다.
그래서 p-value가 필요하다.
1-(p-value)는 대립가설이 맞을 확률이 아니다¶
p-value와 대립가설은 관련이 없다.
순전히 '귀무가설이 맞다는 전제 하에' 나온 값이 p-value이고, p-value를 구함에 있어 대립가설은 그 어디에서도 작용하지 않는다.
유의수준 significance level(alpha)은 p-value에 의해 결정되는 것이 아님¶
alpha는 연구자의 주관이며, 관례적으로 0.05, 0.01 을 사용
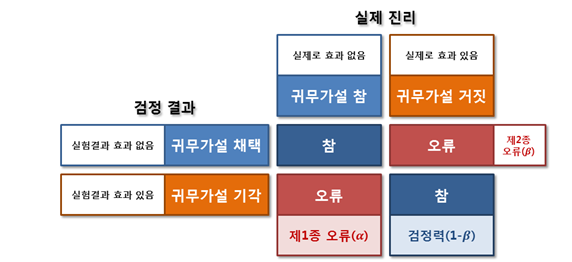
제 1종 오류(Type I Error)
- 맞는 가설을 틀렸다고 증명하는 경우
- 귀무가설이 맞음에도 불구하고 너무 희귀한 검정통계량이 나오는 바람에 맞는 귀무가설을 기각하는 오류
- 제 1종 오류를 범할 확률은 유의수준과 동일
제 2종 오류(Type II Error, Beta)
- 귀무 가설이 거짓인데 기각하지 않음
- 귀무가설이 틀림에도 불구하고 귀무가설하의 확률분포에서 있을 법한 검정통계량이 나오는 바람에 틀린 귀무가설을 채택하는 오류
검정력(1-Beta)
- 검정력이 좋아지면 제 2종 오류를 범할 확률은 낮아짐
제 1종 오류와 2종 오류를 아래 그림으로 이해해 보자.¶
# -*- coding: utf-8 -*-
import seaborn as sns
import pandas as pd
import scipy as sp
import matplotlib as mpl
import matplotlib.pylab as plt
import numpy as np
%matplotlib inline
from matplotlib.patches import Polygon
x = np.linspace(-3.5, 6, 100)
y1 = sp.stats.norm.pdf(x, loc=0)
y2 = sp.stats.norm.pdf(x, loc=4)
plt.figure(figsize=(12,6))
plt.plot(x, y1, linewidth=2)
plt.plot(x, y2, linewidth=2)
ix1 = np.linspace(2, 3.5, 100)
iy1 = sp.stats.norm.pdf(ix1, loc=0)
verts1 = [(2, 0)] + list(zip(ix1, iy1)) + [(3.5, 0)]
poly1 = Polygon(verts1)
plt.gca().add_patch(poly1)
# plt.annotate ← 글자와 화살표 추가
## xytext=(a, b) -> 글자 위치, xy=(a, b) -> 가리킬 포인트 위치
plt.annotate("Type I Error", xytext=(3, 0.05), xy=(2.5, 0.02), horizontalalignment='left', fontsize=20, arrowprops=dict(arrowstyle="->", linewidth=2))
ix2 = np.linspace(0, 2, 100)
iy2 = sp.stats.norm.pdf(ix2, loc=4)
verts2 = [(0, 0)] + list(zip(ix2, iy2)) + [(2, 0)]
poly2 = Polygon(verts2, facecolor='g')
plt.gca().add_patch(poly2)
plt.annotate("Type II Error", xytext=(0, 0.05), xy=(1.5, 0.02), horizontalalignment='center', fontsize=20, arrowprops=dict(arrowstyle="->", linewidth=2))
유의확률(P-value)에 대한 예를 살펴 보자.¶
xx1 = np.linspace(-4, 4, 100)
xx2 = np.linspace(-4, -2, 100)
xx3 = np.linspace(2, 4, 100)
plt.figure(figsize=(15,6))
plt.subplot(3, 1, 1)
plt.fill_between(xx1, sp.stats.norm.pdf(xx1), facecolor='green', alpha=0.1)
plt.fill_between(xx2, sp.stats.norm.pdf(xx2), facecolor='blue', alpha=0.35)
plt.fill_between(xx3, sp.stats.norm.pdf(xx3), facecolor='blue', alpha=0.35)
plt.text(-3, 0.1, "p-value=%5.3f" % (2*sp.stats.norm.cdf(-2)), horizontalalignment='center')
plt.title(r"Test statistics = 2. Two-tailed test. $H_a: \mu \neq 0$")
plt.subplot(3, 1, 2)
plt.fill_between(xx1, sp.stats.norm.pdf(xx1), facecolor='green', alpha=0.1)
plt.fill_between(xx3, sp.stats.norm.pdf(xx3), facecolor='blue', alpha=0.35)
plt.text(3, 0.1, "p-value=%5.3f" % (sp.stats.norm.cdf(-2)), horizontalalignment='center')
plt.title(r"Test statistics = 2. One-tailed test. $H_a: \mu > 0$")
plt.subplot(3, 1, 3)
plt.fill_between(xx1, sp.stats.norm.pdf(xx1), facecolor='green', alpha=0.1)
plt.fill_between(xx2, sp.stats.norm.pdf(xx2), facecolor='blue', alpha=0.35)
plt.text(-3, 0.1, "p-value=%5.3f" % (sp.stats.norm.cdf(-2)), horizontalalignment='center')
plt.title(r"Test statistics = -2. One-tailed test. $H_a: \mu < 0$")
plt.tight_layout()
plt.show()
유의 확률(p-value)의 값이 작으므로 귀무가설은 기각된다.¶
유의 수준과 기각역¶
유의수준(level of significance)¶
계산된 유의 확률 값에 대해 귀무 가설을 기각하는지 채택하는지를 결정할 수 있는 기준 값
일반적으로 사용되는 유의 수준은 1%, 5%, 10% $$\alpha = 0.01,\;\; 0.05,\;\; 0.1$$
유의 수준과 유의 확률을 비교 후 판단
기각역(critical value)¶
특정한 유의 확률 값에 대해 해당하는 검정 통계량
기각역과 검정 통계량을 비교 후 판단
- 기각역 값을 알고 있다면 검정 통계량을 비교하여 기각/채택 여부를 판단할 수 있다.
신뢰 수준(confidence level)¶
1 - alpha → 신뢰 수준
alpha = 0.01 → 신뢰 수준 99%
alpha = 0.05 → 신뢰 수준 95%
이제 가설과 검정 ① 서두에서 제기한 문제를 다시 풀어보자.¶
$$ \text{Bin}(n \geq 12;N=15) = 0.017578125 $$문제1
- 어떤 동전을 15번 던졌더니 12번이 앞면이 나왔다. 이 동전은 휘어지지 않은 공정한 동전(fair coin, 앞 뒤 확률이 각 각 0.5)인가?
여기서 검정 통계량은 15번 던져 앞면이 나온 횟수가 12이고 이 값은 자유도가 15인 이항 분포를 따른다.
이 경우의 유의 확률(p-value) = 1.76% 이다.
# N = 15, n = 12, p = 0.5
## sp.stats.binom(N, P).cdf(n-1)
1 - sp.stats.binom(15, 0.5).cdf(12-1)
이 값은 5% 보다는 작고 1% 보다는 크기 때문에 유의 수준이 5% 라면 귀무가설을 기각할 수 있으며(즉, 공정한 동전이 아니라고 말할 수 있다.)¶
단, 유의 수준이 0.01 이라면 기각할 수 없다.(즉, 공정한 동전이 아니라고 말할 수 없다.)
- 문제2
어떤 트레이더의 일주일 수익률은 다음과 같다.
- 2.5%, -5%, 4.3%, -3.7% -5.6%
- 이 트레이더는 돈을 벌어다 줄 사람인가, 아니면 돈을 잃을 사람인가?
$$ t = \dfrac{\bar{x}}{s\;/\sqrt{N}} = -1.4025 $$수익률이 정규 분포를 따른 다고 가정하면 이 트레이더의 검정통계량은 다음과 같이 계산된다.
$$ F(t=-1.4025;4) = 0.1167 $$이 검정 통계량에 대한 유의 확률은 11.67%이다.
x = np.array([-0.025, -0.05, 0.043, -0.037, -0.056])
t = x.mean()/x.std(ddof=1)*np.sqrt(len(x))
t, sp.stats.t(df=4).cdf(t)